Support Vector Machines (SVM)

In this sample, you will learn how to use the OpenCV function cv.SVM.train to build a classifier based on SVMs and cv.SVM.predict to test its performance.

Sources:

Introduction to Support Vector Machines
Support Vector Machines for Non-Linearly Separable Data
Code

Introduction to Support Vector Machines

A Support Vector Machine (SVM) is a discriminative classifier formally defined by a separating hyperplane. In other words, given labeled training data (supervised learning), the algorithm outputs an optimal hyperplane which categorizes new examples.

In which sense is the hyperplane obtained optimal? Let's consider the following simple problem; For a linearly separable set of 2D-points which belong to one of two classes, find a separating straight line.

Note: In this example we deal with lines and points in the Cartesian plane instead of hyperplanes and vectors in a high dimensional space. This is a simplification of the problem. It is important to understand that this is done only because our intuition is better built from examples that are easy to imagine. However, the same concepts apply to tasks where the examples to classify lie in a space whose dimension is higher than two.

In the above picture you can see that there exists multiple lines that offer a solution to the problem. Is any of them better than the others? We can intuitively define a criterion to estimate the worth of the lines: A line is bad if it passes too close to the points because it will be noise sensitive and it will not generalize correctly. Therefore, our goal should be to find the line passing as far as possible from all points.

Then, the operation of the SVM algorithm is based on finding the hyperplane that gives the largest minimum distance to the training examples. Twice, this distance receives the important name of margin within SVM's theory. Therefore, the optimal separating hyperplane maximizes the margin of the training data.

To undertand how the optimal hyperplane is computed, let's introduce the notation used to define formally a hyperplane:

$f(x) = \beta_{0} + \beta^{T} x$

where $\beta$ is known as the weight vector and $\beta_{0}$ as the bias.

For a more in-depth description of this and hyperplanes you can find in the section 4.5 (Seperating Hyperplanes) of the book:

"Elements of Statistical Learning" by T. Hastie, R. Tibshirani and J. H. Friedman.

The optimal hyperplane can be represented in an infinite number of different ways by scaling of $\beta$ and $\beta_{0}$ . As a matter of convention, among all the possible representations of the hyperplane, the one chosen is:

$|\beta_{0} + \beta^{T} x| = 1$

where symbolizes the training examples closest to the hyperplane. In general, the training examples that are closest to the hyperplane are called support vectors. This representation is known as the canonical hyperplane.

Now, we use the result of geometry that gives the distance between a point and a hyperplane $(\beta, \beta_{0})$ :

$\mathrm{distance} = \frac{|\beta_{0} + \beta^{T} x|}{||\beta||}$

In particular, for the canonical hyperplane, the numerator is equal to one and the distance to the support vectors is:

$\mathrm{distance}_{\textrm{support vectors}} = \frac{|\beta_{0} + \beta^{T} x|}{||\beta||} = \frac{1}{||\beta||}$

Recall that the margin introduced in the previous section, here denoted as , is twice the distance to the closest examples:

$M = \frac{2}{||\beta||}$

Finally, the problem of maximizing is equivalent to the problem of minimizing a function $L(\beta)$ subject to some constraints. The constraints model the requirement for the hyperplane to classify correctly all the training examples $x_{i}$ . Formally,

$\min_{\beta, \beta_{0}} L(\beta) = \frac{1}{2}||\beta||^{2} \\ \quad \textrm{subject to} \quad y_{i}(\beta^{T} x_{i} + \beta_{0}) \geq 1 \; \forall i$

where $y_{i}$ represents each of the labels of the training examples.

This is a problem of Lagrangian optimization that can be solved using Lagrange multipliers to obtain the weight vector $\beta$ and the bias $\beta_{0}$ of the optimal hyperplane.

Support Vector Machines for Non-Linearly Separable Data

Why is it interesting to extend the SVM optimation problem in order to handle non-linearly separable training data? Most of the applications in which SVMs are used in computer vision require a more powerful tool than a simple linear classifier. This stems from the fact that in these tasks the training data can be rarely separated using an hyperplane.

Consider one of these tasks, for example, face detection. The training data in this case is composed by a set of images that are faces and another set of images that are non-faces (every other thing in the world except from faces). This training data is too complex so as to find a representation of each sample (feature vector) that could make the whole set of faces linearly separable from the whole set of non-faces.

Remember that using SVMs we obtain a separating hyperplane. Therefore, since the training data is now non-linearly separable, we must admit that the hyperplane found will misclassify some of the samples. This misclassification is a new variable in the optimization that must be taken into account. The new model has to include both the old requirement of finding the hyperplane that gives the biggest margin and the new one of generalizing the training data correctly by not allowing too many classification errors.

We start here from the formulation of the optimization problem of finding the hyperplane which maximizes the margin:

$\min_{\beta, \beta_{0}} L(\beta) = \frac{1}{2}||\beta||^{2} \\ \quad \textrm{subject to} \quad y_{i}(\beta^{T} x_{i} + \beta_{0}) \geq 1 \; \forall i$

There are multiple ways in which this model can be modified so it takes into account the misclassification errors. For example, one could think of minimizing the same quantity plus a constant times the number of misclassification errors in the training data, i.e.:

$\min ||\beta||^{2} + C \textrm{(\# misclassication errors)}$

However, this one is not a very good solution since, among some other reasons, we do not distinguish between samples that are misclassified with a small distance to their appropriate decision region or samples that are not. Therefore, a better solution will take into account the distance of the misclassified samples to their correct decision regions, i.e.:

$\min ||\beta||^{2} + C \textrm{(distance of misclassified samples to their correct regions)}$

For each sample of the training data a new parameter $\xi_{i}$ is defined. Each one of these parameters contains the distance from its corresponding training sample to their correct decision region. The following picture shows non-linearly separable training data from two classes, a separating hyperplane and the distances to their correct regions of the samples that are misclassified.

Note: Only the distances of the samples that are misclassified are shown in the picture. The distances of the rest of the samples are zero since they lay already in their correct decision region.

The red and blue lines that appear on the picture are the margins to each one of the decision regions. It is very important to realize that each of the $\xi_{i}$ goes from a misclassified training sample to the margin of its appropriate region.

Finally, the new formulation for the optimization problem is:

$\min_{\beta, \beta_{0}} L(\beta) = ||\beta||^{2} + C \sum_{i} {\xi_{i}} \\ \quad \textrm{subject to} \quad y_{i}(\beta^{T} x_{i} + \beta_{0}) \geq 1 - \xi_{i} \\ \quad \textrm{and} \quad \xi_{i} \geq 0 \; \forall i$

How should the parameter be chosen? It is obvious that the answer to this question depends on how the training data is distributed. Although there is no general answer, it is useful to take into account these rules:

Large values of C give solutions with less misclassification errors but a smaller margin. Consider that in this case it is expensive to make misclassification errors. Since the aim of the optimization is to minimize the argument, few misclassifications errors are allowed.
Small values of C give solutions with bigger margin and more classification errors. In this case the minimization does not consider that much the term of the sum so it focuses more on finding a hyperplane with big margin.

In addition to the problem of misclassification, another intuition can be observed. There is a chance that for a non-linear separable data in lower-dimensional space to become linearly separable if mapped to a higher-dimensional space.

In general, it is possible to map points in a d-dimensional space to some D-dimensional space to check the possibility of linear separability. There is an idea which helps to compute the dot product in the high-dimensional (kernel) space by performing computations in the low-dimensional input (feature) space. We can illustrate with following example.

Consider two points in two-dimensional space, and . Let $\phi$ be a mapping function which maps a two-dimensional point to three-dimensional space as follows:

$\phi(p) = (p_{1}^2, p_{2}^2, \sqrt{2} p_1 p_2)$

$\phi(q) = (q_{1}^2, q_{2}^2, \sqrt{2} q_1 q_2)$

Let us define a kernel function which does a dot product between two points, shown below:

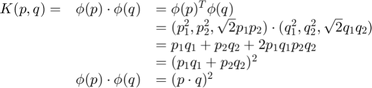
$\begin{array}{lll} K(p,q) = & \phi(p) \cdot \phi(q) & = \phi(p)^T \phi(q) \\ & & = (p_{1}^2,p_{2}^2,\sqrt{2} p_1 p_2) \cdot (q_{1}^2,q_{2}^2,\sqrt{2} q_1 q_2) \\ & & = p_1 q_1 + p_2 q_2 + 2 p_1 q_1 p_2 q_2 \\ & & = (p_1 q_1 + p_2 q_2)^2 \\ & \phi(p) \cdot \phi(q) & = (p \cdot q)^2 \end{array}$

It means, a dot product in three-dimensional space can be achieved using squared dot product in two-dimensional space. This can be applied to higher dimensional space. So we can calculate higher dimensional features from lower dimensions itself. Once we map them, we get a higher dimensional space.

For additional resources, refer to:

NPTEL notes on Statistical Pattern Recognition, Chapters 25-29

Code

Set up training data, formed by a set of labeled 2D-points that belong to one of two different classes. (data is a floating-point matrix, and labels are integer for classification)

H = 512; W = 512;
if false
    % 200 random points generated from two normal distributions
    data = [
        bsxfun(@plus, bsxfun(@times, randn(100,2), [W H]*0.1), [W H]*0.4);
        bsxfun(@plus, bsxfun(@times, randn(100,2), [W H]*0.1), [W H]*0.6)
    ];
    labels = [ones(100,1); -ones(100,1)];
elseif true
    % the training data is generated randomly using a uniform probability
    % density functions (PDFs) in two parts. First we generate data for both
    % classes that is linearly separable. Next we create data for both classes
    % that is non-linearly separable (data that overlaps).
    %
    % * 90 points in [0.0, 0.4] for class1
    % * 20 points in [0.4, 0.6] for class1 and class2
    % * 90 points in [0.6, 1.0] for class2
    X = [rand(90,1)*0.4; rand(20,1)*0.2+0.4; rand(90,1)*0.4+0.6] * W;
    Y = rand(size(X)) * H;
    data = [X Y];
    labels = [ones(100,1); -ones(100,1)];
else
    % one point from one class, and three points from the other
    data = [501 10; 255 10; 501 255; 10 501];
    labels = [1; -1; -1; -1];
end
labels = int32(labels);

L = unique(labels);  % [-1, +1]
whos data labels
if ~mexopencv.isOctave() && mexopencv.require('stats')
    %HACK: tabulate in Octave behaves differently
    tabulate(labels)
end

  Name          Size            Bytes  Class     Attributes

  data        200x2              3200  double              
  labels      200x1               800  int32               

  Value    Count   Percent
     -1      100     50.00%
      1      100     50.00%

Create SVM classifier, and set up its parameters. SVM can be applied in a wide variety of problems (with non-linearly separable data). In such case a kernel function is often used to raise the dimensionality of the examples. First, we have to define some parameters before training the SVM.

svm = cv.SVM();

Type of SVM: We choose here the C_SVC type that can be used for n-class classification ( $n \geq 2$ ). The important feature of this type is that it deals with imperfect separation of classes (i.e. when the training data is non-linearly separable).

svm.Type = 'C_SVC';

Type of SVM kernel: We have not yet talked about kernel functions. Briefly it is a mapping done to the training data to improve its resemblance to a linearly separable set of data. This mapping consists of increasing the dimensionality of the data and is done efficiently using a kernel function. If you choose the Linear type, it means that no mapping is done.

if false
    svm.KernelType = 'Linear';
elseif true
    svm.KernelType = 'RBF';
else
    svm.KernelType = 'Poly';
    svm.Degree = 2;
end

Termination criteria of the algorithm: The SVM training procedure is implemented solving a constrained quadratic optimization problem in an iterative fashion. Here we specify a maximum number of iterations and a tolerance error so we allow the algorithm to finish in less number of steps even if the optimal hyperplane has not been reached yet. To correctly solve a problem with non-linearly separable training data, the maximum number of iterations has to be increased considerably.

svm.TermCriteria.maxCount = 50000;

C: In the non-linearly separable data example, chose a small value of this parameter in order not to punish too much the misclassification errors in the optimization. The idea of doing this stems from the will of obtaining a solution close to the one intuitively expected. However, we recommend to get a better insight of the problem by making adjustments to this parameter. In this example there are just very few points in the overlapping region between classes. If you increase the density of overlapping points, the impact of the parameter C can be shown.
Gamma: the inverse of the standard deviation of the Gaussian RBF kernel.

We can either use fixed value for these parameters, or find optimal ones using cross-validation by searching over a grid of values.

auto_opts = {'DegreeGrid',[0 0 0], 'PGrid',[0 0 0], 'NuGrid',[0 0 0]};
if true
    % specify search grid (user-supplied min/max/logstep, or default grid)
    auto_opts = [auto_opts, 'CGrid',[0.1 500 5], 'GammaGrid','Gamma'];
else
    % set a fixed param value, and disable grid searching
    svm.C = 50;
    svm.Gamma = 5e-4;
    auto_opts = [auto_opts, 'CGrid',[0 0 0], 'GammaGrid',[0 0 0]];
end

Train the SVM

tic
if true
    svm.trainAuto(data, labels, 'KFold',5, 'Balanced',true, auto_opts{:});
else
    svm.train(data, labels);
end
toc
display(svm)

Elapsed time is 0.059405 seconds.
svm = 
  SVM with properties:

              id: 5
            Type: 'C_SVC'
      KernelType: 'RBF'
          Degree: 0
           Gamma: 1.0000e-05
           Coef0: 0
               C: 2.5000
              Nu: 0
               P: 0
    ClassWeights: []
    TermCriteria: [1×1 struct]

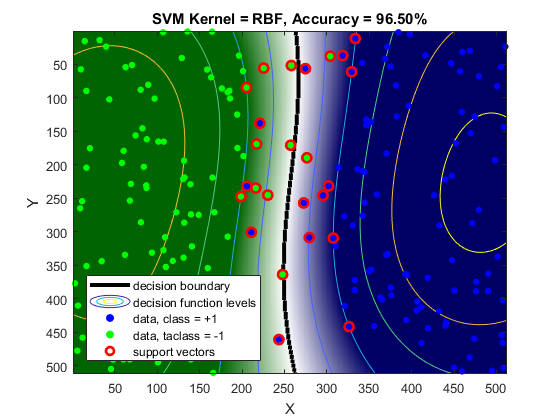
Test performance on training data

acc = nnz(svm.predict(data) == labels) / numel(labels);
display(acc)

acc =
    0.9650

Options for visualization

clrBG = [0 0 100; 0 100 0];
clrFG = [0 0 255; 0 255 0];

Draw the decision regions given by the SVM. The predict method is used to classify an input sample using a trained SVM. In this example we have used this method in order to color the space depending on the prediction done by the SVM. In other words, an image is traversed interpreting its pixels as points of the Cartesian plane. Each of the points is colored depending on the class predicted by the SVM; in dark green if it was classified as class with positive label and in dark blue if it was classified as negative label. This results in a division of the image in a blue region and a green region. The boundary between both regions is the optimal separating hyperplane.

[X,Y] = meshgrid(1:W, 1:H);
C = svm.predict([X(:) Y(:)]);
C = reshape(C, size(X));
img = uint8(cat(3, C*0, C==+1, C==-1) * 100);

Draw the training data. Points of positive class are represented with bright green circles, while bright blue circles are used for the negative class. In the case of non-linearly separable data with a linear classifier, it can be seen that some of the examples of both classes are misclassified; some green points lay on the blue region and some blue points lay on the green one.

for i=1:numel(L)
    img = cv.circle(img, data(labels == L(i),:), 3, ...
        'Color',clrFG(i,:), 'Thickness','Filled');
end

Draw support vectors. We obtain a list of all training examples that are support vectors and highlight them in gray rings.

if strcmp(svm.KernelType, 'Linear')
    sv = svm.getUncompressedSupportVectors();
else
    sv = svm.getSupportVectors();
end
img = cv.circle(img, sv, 6, 'Color',[128 128 128], 'Thickness',2);

Show result

imshow(img), title('SVM')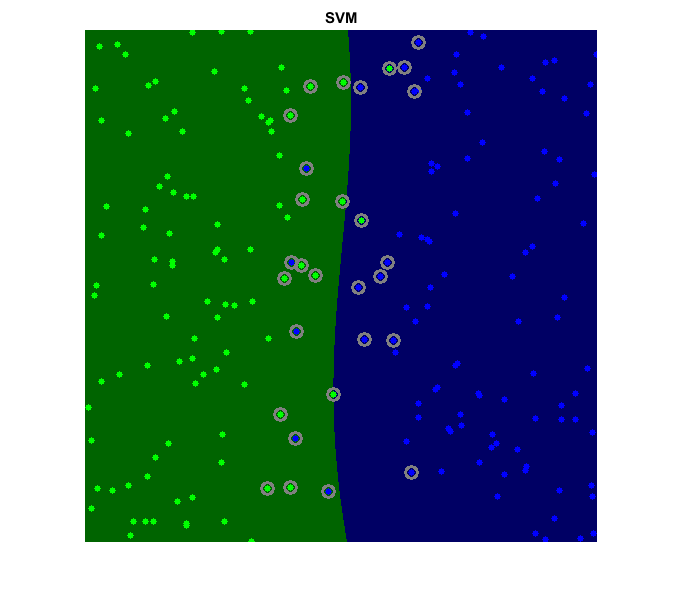

Compute classification confidence (decision function value which is the signed distance to the margin)

conf = svm.predict([X(:) Y(:)], 'RawOutput',true);
conf = reshape(abs(conf), size(X));

More advanced visualization

img = zeros(size(C));
for i=1:numel(L)
    img(C == L(i)) = i;
end
img = ind2rgb(img, clrBG/255);

figure, hImg = image(img);
if ~mexopencv.isOctave()
    %HACK: transparency not yet implemented in Octave
    set(hImg, 'AlphaData',conf);
end
hold on
contour(C, [0 0], 'LineWidth',3, 'LineColor','k')
contour(conf, 'LineWidth',0.5)
for i=1:numel(L)
    idx = (labels == L(i));
    scatter(data(idx,1), data(idx,2), 24, clrFG(i,:)/255, 'filled')
end
scatter(sv(:,1), sv(:,2), 48, [255 0 0]/255, 'LineWidth',2)
hold off, xlabel('X'), ylabel('Y')
title(sprintf('SVM Kernel = %s, Accuracy = %.2f%%', svm.KernelType, acc*100))
set(gca, 'Color',mean(clrBG)/255)
legend({'decision boundary', 'decision function levels', ...
    'data, class = +1', 'data, taclass = -1', 'support vectors'}, ...
    'Color','w', 'Location','Southwest')

Support Vector Machines (SVM)

Contents

Introduction to Support Vector Machines

Support Vector Machines for Non-Linearly Separable Data

Code