Camera Calibration

This example demonstrates camera calibration in OpenCV. It shows usage of the following functions:

cv.findChessboardCorners, cv.findCirclesGrid
cv.cornerSubPix
cv.drawChessboardCorners
cv.initCameraMatrix2D
cv.calibrateCamera
cv.projectPoints
cv.getOptimalNewCameraMatrix
cv.initUndistortRectifyMap, cv.remap
cv.undistort
cv.Rodrigues

You can find more test images at these locations:

Cameras have been around for a long-long time. However, with the introduction of the cheap pinhole cameras in the late 20th century, they became a common occurrence in our everyday life. Unfortunately, this cheapness comes with its price: significant distortion. Luckily, these are constants and with a calibration and some remapping we can correct this. Furthermore, with calibration you may also determine the relation between the camera's natural units (pixels) and the real world units (for example millimeters).

In the sample, we will learn:

about distortions in camera, intrinsic and extrinsic parameters of camera
how to find these parameters, undistort images, etc.

Sources:

Theory
Code

Theory

Two major distortions OpenCV takes into account are radial distortion and tangential distortion. For the radial factor one uses the following formula:

$\begin{array}{l} x_{distorted} = x( 1 + k_1 r^2 + k_2 r^4 + k_3 r^6) \cr y_{distorted} = y( 1 + k_1 r^2 + k_2 r^4 + k_3 r^6) \end{array}$

So for an undistorted pixel point at coordinates, its position on the distorted image will be $(x_{distorted}, y_{distorted})$ . The presence of the radial distortion manifests in form of the "barrel" or "fish-eye" effect.

Due to radial distortion, straight lines will appear curved. Its effect is more as we move away from the center of image. For example, one image is shown below, where two edges of a chess board are marked with red lines. But you can see that border is not a straight line and doesn't match with the red line. All the expected straight lines are bulged out. See Distortion for more details.

Tangential distortion occurs because the image taking lenses are not perfectly parallel to the imaging plane. So some areas in image may look nearer than expected. It can be represented via the formulas:

$\begin{array}{l} x_{distorted} = x + [ 2p_1xy + p_2(r^2+2x^2)] \cr y_{distorted} = y + [ p_1(r^2+ 2y^2)+ 2p_2xy] \end{array}$

So we have five distortion parameters which in OpenCV are presented as one row matrix with 5 columns:

$distortion\_coefficients = (k_1, k_2, p_1, p_2, k_3)$

In addition to this, we need to find a few more information, like intrinsic and extrinsic parameters of a camera. Intrinsic parameters are specific to a camera. Extrinsic parameters corresponds to rotation and translation vectors which translates a coordinates of a 3D point to a coordinate system.

Now for the unit conversion we use the following formula:

$\left[ {\matrix{ x \cr y \cr w }} \right] = \left[ {\matrix{ f_x & 0 & c_x \cr 0 & f_y & c_y \cr 0 & 0 & 1 }} \right] \left[ {\matrix{ X \cr Y \cr Z }} \right]$

Here the presence of is explained by the use of homography coordinate system (and ). The unknown parameters are and (camera focal lengths) and which are the optical centers expressed in pixels coordinates. If for both axes a common focal length is used with a given aspect ratio (usually 1), then and in the upper formula we will have a single focal length . The matrix containing these four parameters is referred to as the camera matrix. While the distortion coefficients are the same regardless of the camera resolutions used, these should be scaled along with the current resolution from the calibrated resolution.

The process of determining these two matrices is the calibration. Calculation of these parameters is done through basic geometrical equations. The equations used depend on the chosen calibrating objects with well defined pattern. Currently OpenCV supports three types of objects for calibration:

Classical black-white chessboard
Symmetrical circle pattern
Asymmetrical circle pattern

Basically, you need to take snapshots of these patterns with your camera and let OpenCV find them. Each found pattern results in a new equation (we know its coordinates in real world space and we know its coordinates found in image). To solve the equation you need at least a predetermined number of pattern snapshots to form a well-posed equation system. This number is higher for the chessboard pattern and less for the circle ones. For example, in theory the chessboard pattern requires at least two snapshots. However, in practice we have a good amount of noise present in our input images, so for good results you will probably need at least 10 good snapshots of the input pattern in different positions.

We do the calibration with the help of the cv.calibrateCamera function. It has the following arguments:

The object points. This is a cell array of Nx3 points that for each input image describes how should the pattern look. If we have a planar pattern (like a chessboard) then we can simply set all Z coordinates to zero. This is a collection of the points where these important points are present. Because, we use a single pattern for all the input images we can calculate this just once and repeat it for all the other input views. We calculate the corner points with the calcBoardCorners function.
The image points. This is a cell arrray of Nx2 points which for each input image contains coordinates of the important points (corners for chessboard and centers of the circles for the circle pattern). We have already collected this from cv.findChessboardCorners or cv.findCirclesGrid function. We just need to pass it on.
The size of the image.
The camera matrix. If we used the fixed aspect ratio option we need to set .
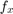The distortion coefficient matrix, initialized with zeros.
The final argument is the flag. You need to specify here options like fix the aspect ratio for the focal length, assume zero tangential distortion or to fix the principal point.
For all the views, the function will calculate rotation and translation arrays which transform the object points (given in the model coordinate space) to the image points (given in the world coordinate space). The output cell array of matrices containing in the i-th position the rotation and translation vector for the i-th object point to the i-th image point.
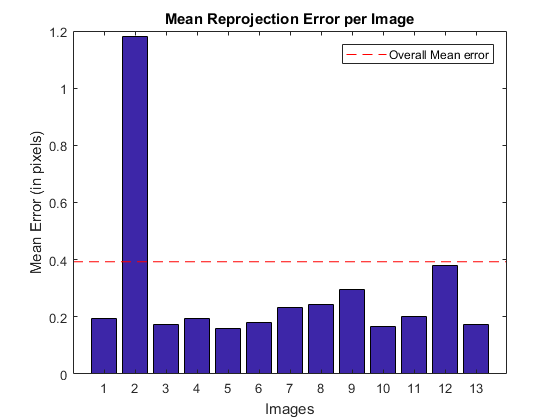
The function returns the average re-projection error. This number gives a good estimation of precision of the found parameters. This should be as close to zero as possible. Given the intrinsic, distortion, rotation and translation matrices we may calculate the error for one view by using the cv.projectPoints to first transform the object point to image point. Then we calculate the absolute norm between what we got with our transformation and the corner/circle finding algorithm. To find the average error we calculate the arithmetical mean of the errors calculated for all the calibration images.

You may watch a video of the camera calibration on YouTube.

Once calibration is done, we can undistort images and correct them for the lens distortion. For example, you can see in the result below that all the edges become straight.

Code

function varargout = calibration_demo()

Options and calibration flags (keep in mind that the number of images needed grows dramatically with the number of parameters we are solving for, i.e distortion coeffs)

    opts = struct();
    opts.aspectRatio = 1;                 % aspect ratio (ar = fx/fy)
    opts.flags.UseIntrinsicGuess = false; % how to initize camera matrix
    opts.flags.FixAspectRatio = true;     % fix aspect ratio (ar = fx/fy)
    opts.flags.FixFocalLength = false;    % fix fx and fy
    opts.flags.FixPrincipalPoint = false; % fix principal point at the center
    opts.flags.ZeroTangentDist = false;   % assume zero tangential distortion
    opts.flags.RationalModel = false;     % enable (k4,k5,k6)
    opts.flags.ThinPrismModel = false;    % enable (s1,s2,s3,s4)
    opts.flags.TiltedModel = false;       % enable (taux,tauy)
    %opts.flags.FixK3 = true;
    %opts.flags.FixK4 = true;
    %opts.flags.FixK5 = true;

list of board images

    opts.pattern = 'chessboard'; % type of pattern grid: chessboard, acircles, circles
    opts.boardSize = [9 6];      % number of inner corners per board dimensions
    opts.squareSize = 30.0;      % board square size in millimeters
    files = cv.glob(fullfile(mexopencv.root(), 'test', 'left*.jpg'));
    finfo = imfinfo(files{1});
    opts.imageSize = [finfo.Width, finfo.Height];
    display(opts);
    display(files(:));

opts = 
  struct with fields:

    aspectRatio: 1
          flags: [1×1 struct]
        pattern: 'chessboard'
      boardSize: [9 6]
     squareSize: 30
      imageSize: [640 480]
  13×1 cell array
    'C:\Users\Amro\Desktop\mexopencv\test\left01.jpg'
    'C:\Users\Amro\Desktop\mexopencv\test\left02.jpg'
    'C:\Users\Amro\Desktop\mexopencv\test\left03.jpg'
    'C:\Users\Amro\Desktop\mexopencv\test\left04.jpg'
    'C:\Users\Amro\Desktop\mexopencv\test\left05.jpg'
    'C:\Users\Amro\Desktop\mexopencv\test\left06.jpg'
    'C:\Users\Amro\Desktop\mexopencv\test\left07.jpg'
    'C:\Users\Amro\Desktop\mexopencv\test\left08.jpg'
    'C:\Users\Amro\Desktop\mexopencv\test\left09.jpg'
    'C:\Users\Amro\Desktop\mexopencv\test\left11.jpg'
    'C:\Users\Amro\Desktop\mexopencv\test\left12.jpg'
    'C:\Users\Amro\Desktop\mexopencv\test\left13.jpg'
    'C:\Users\Amro\Desktop\mexopencv\test\left14.jpg'

load images

    N = numel(files);
    imgs = cell(N,1);
    for i=1:N
        imgs{i} = cv.imread(files{i}, 'Color',true);
    end

detect image points, and filter out views where detection failed

    [imagePoints, found] = detectImageCorners(imgs, opts);
    if ~all(found)
        files = files(found);
        imgs = imgs(found);
        imagePoints = imagePoints(found);
        found = found(found);
        N = nnz(found);
        assert(N >= 2, 'Not enough views');
    end

show detected corners

    for i=1:N
        img = cv.drawChessboardCorners(imgs{i}, opts.boardSize, ...
            imagePoints{i}, 'PatternWasFound',found(i));
        imshow(img), title(sprintf('Detection, %d/%d', i, N))
        pause(1)
    end

create object points (we assume a fully visible calibration pattern, the same shown in each view)

    objectPoints = calcBoardCorners(opts);
    objectPoints = repmat({objectPoints}, N, 1);

run calibration

    [calib, ok] = runCalibration(objectPoints, imagePoints, opts);
    if ~ok
        disp('calibration failed');
        return;
    end
    fprintf('avg reprojection error = %f\n', calib.rms)

    %
    % save intrinsic/extrinsic parameters
    fname = fullfile(tempdir(), sprintf('calibration_%s.yml', opts.pattern));
    saveCameraParams(fname, calib, opts);  % ..., true, imagePoints
    fprintf('Saved to: %s\n', fname);

avg reprojection error = 0.392591
Saved to: C:\Users\Amro\AppData\Local\Temp\calibration_chessboard.yml

display parameter estimation errors

    displayErrorEstimates(calib);

			Standard Errors of Estimated Camera Parameters
			----------------------------------------------

Intrinsics
----------
Focal length (pixels):    [  535.9158 +/- 0.0000      535.9158 +/- 1.2919    ]
Principal Point (pixels): [  342.2831 +/- 1.3643      235.5708 +/- 1.4770    ]
Radial distortion:        [   -0.2664 +/- 0.0163       -0.0386 +/- 0.1271        0.2384 +/- 0.2763    ]
Tangential distortion:    [    0.0018 +/- 0.0003       -0.0003 +/- 0.0004    ]
Rational distortion:      [    0.0000 +/- 0.0000        0.0000 +/- 0.0000        0.0000 +/- 0.0000    ]
Thin Prism distortion:    [    0.0000 +/- 0.0000        0.0000 +/- 0.0000        0.0000 +/- 0.0000        0.0000 +/- 0.0000    ]
Tilt distortion:          [    0.0000 +/- 0.0000        0.0000 +/- 0.0000    ]

Extrinsics
----------
Rotation vectors:
	[    0.1687 +/- 0.0045        0.2757 +/- 0.0037        0.0135 +/- 0.0007    ]
	[    0.4133 +/- 0.0030        0.6499 +/- 0.0030       -1.3372 +/- 0.0011    ]
	[   -0.2770 +/- 0.0032        0.1869 +/- 0.0029        0.3549 +/- 0.0006    ]
	[   -0.1109 +/- 0.0035        0.2397 +/- 0.0031       -0.0021 +/- 0.0006    ]
	[   -0.2919 +/- 0.0032        0.4284 +/- 0.0031        1.3127 +/- 0.0008    ]
	[    0.4078 +/- 0.0045        0.3037 +/- 0.0048        1.6491 +/- 0.0010    ]
	[    0.1793 +/- 0.0043        0.3456 +/- 0.0042        1.8685 +/- 0.0011    ]
	[   -0.0910 +/- 0.0034        0.4798 +/- 0.0036        1.7534 +/- 0.0009    ]
	[    0.2030 +/- 0.0033       -0.4239 +/- 0.0029        0.1324 +/- 0.0008    ]
	[   -0.4191 +/- 0.0031       -0.4997 +/- 0.0031        1.3356 +/- 0.0011    ]
	[   -0.2385 +/- 0.0033        0.3479 +/- 0.0034        1.5308 +/- 0.0008    ]
	[    0.4640 +/- 0.0034       -0.2835 +/- 0.0032        1.2386 +/- 0.0009    ]
	[   -0.1700 +/- 0.0032       -0.4712 +/- 0.0033        1.3460 +/- 0.0009    ]
Translation vectors (world units):
	[  -90.2615 +/- 1.2416     -130.7513 +/- 1.3360      479.6425 +/- 1.2225    ]
	[  -70.2860 +/- 1.0905       99.5110 +/- 1.1628      424.5722 +/- 0.8268    ]
	[  -47.8158 +/- 0.9803     -120.4993 +/- 1.0490      381.7914 +/- 0.9091    ]
	[ -118.0928 +/- 1.0151      -80.7960 +/- 1.1010      397.0229 +/- 0.9889    ]
	[   70.1913 +/- 0.9831     -138.3804 +/- 1.0571      380.6232 +/- 0.8789    ]
	[  200.7249 +/- 1.1203      -78.6852 +/- 1.1897      403.7536 +/- 1.2704    ]
	[   23.4401 +/- 1.2035      -86.1863 +/- 1.2831      467.3153 +/- 1.2198    ]
	[   94.8605 +/- 0.9806     -105.5304 +/- 1.0515      379.9929 +/- 0.9313    ]
	[  -79.6155 +/- 0.8793      -97.2232 +/- 0.9395      333.9627 +/- 0.9948    ]
	[   56.2833 +/- 1.0458     -133.2075 +/- 1.1206      405.6676 +/- 0.9723    ]
	[   60.9174 +/- 0.9959     -123.1165 +/- 1.0639      386.6416 +/- 0.9060    ]
	[   40.4392 +/- 0.9075     -109.9407 +/- 0.9918      349.7354 +/- 1.0263    ]
	[   54.0186 +/- 0.9671     -129.8143 +/- 1.0406      374.9252 +/- 0.9582    ]

reprojection errors

    [calib.rms, calib.rmsPerView, reprojErrs] = computeReprojectionErrors(...
        objectPoints, imagePoints, calib);
    figure, visualizeReprojErrors(calib.rms, calib.rmsPerView, reprojErrs);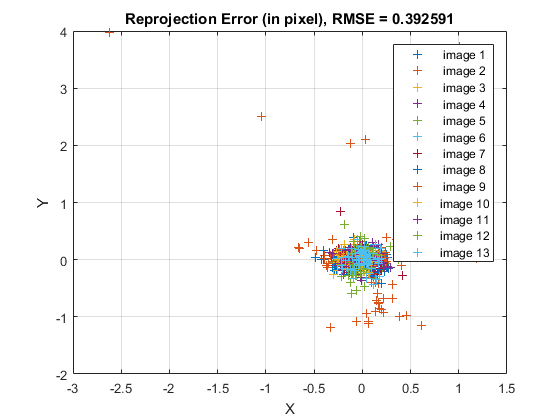

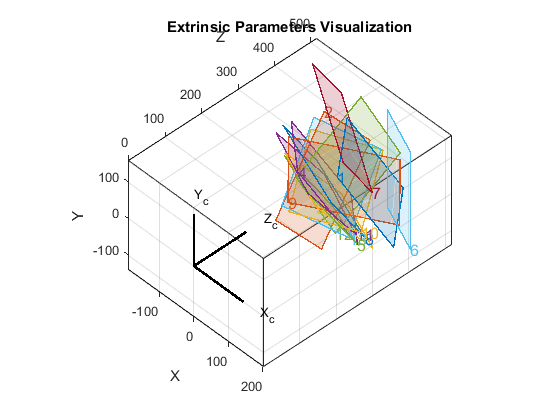
visualize board locations (poses in camera centric view)

    figure, visualizeExtrinsics(calib, opts);

visualize distortion model

    figure, visualizeDistortion(calib, opts);

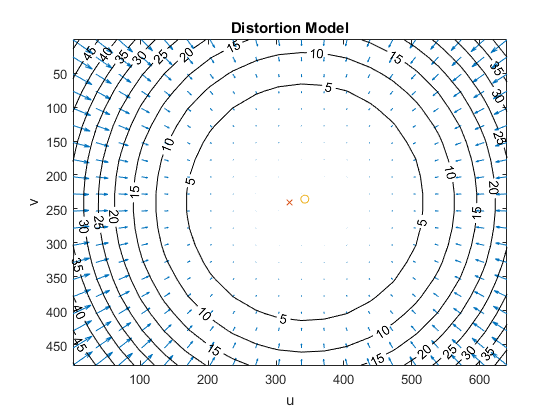
correct images for lens distortion, and show them

    [undistortImage, roi] = buildUndistortFunction(calib, opts);
    figure
    for i=1:N
        img = undistortImage(imgs{i});
        if false
            img = cv.Rect.crop(img, roi);
        end
        imshow(img), title(sprintf('Undistortion, %d/%d', i, N))
        pause(1)
    end

output arguments

    if nargout > 0, varargout{1} = calib; end
    if nargout > 1, varargout{2} = opts; end

end

function [imagePoints, founds] = detectImageCorners(imgs, opts)
    if true
        blobOpts = {};
    else
        % customize blob detector used in findCirclesGrid
        blobOpts = {'BlobDetector',{'SimpleBlobDetector', 'MaxArea',1e4}};
    end

    N = numel(imgs);
    imagePoints = cell(N,1);
    founds = false(N,1);
    for i=1:N
        switch opts.pattern
            case 'chessboard'
                [pts,found] = cv.findChessboardCorners(...
                    imgs{i}, opts.boardSize, 'FastCheck',true);
                if found
                    % improve the found corners coordinate accuracy
                    gray = cv.cvtColor(imgs{i}, 'RGB2GRAY');
                    pts = cv.cornerSubPix(gray, pts, 'WinSize',[11 11], ...
                        'Criteria',struct('type','Count+EPS', ...
                            'maxCount',30, 'epsilon',0.1));
                end
            case 'circles'
                [pts,found] = cv.findCirclesGrid(imgs{i}, opts.boardSize, ...
                    'SymmetricGrid',true, blobOpts{:});
            case 'acircles'
                [pts,found] = cv.findCirclesGrid(imgs{i}, opts.boardSize, ...
                    'SymmetricGrid',false, blobOpts{:});
            otherwise
                pts = {};
                found = false;
        end
        imagePoints{i} = cat(1, pts{:});
        founds(i) = found;
    end
end

function corners = calcBoardCorners(opts)
    % planar calibration pattern (in model coordinate system)
    [X,Y] = ndgrid(1:opts.boardSize(1), 1:opts.boardSize(2));
    switch opts.pattern
        case {'chessboard', 'circles'}
            corners = [X(:), Y(:)];
        case 'acircles'
            corners = [2*X(:) + mod(Y(:),2), Y(:)];
        otherwise
            corners = zeros(0,2);
    end
    corners = (corners - 1) * opts.squareSize;
    corners(:,3) = 0;  % Z = 0
end

function [calib, ok] = runCalibration(objectPoints, imagePoints, opts)
    % calibration flags
    calib = struct();
    if opts.flags.UseIntrinsicGuess
        if opts.flags.FixAspectRatio
            params = {'AspectRatio',opts.aspectRatio};
        else
            params = {'AspectRatio',0};
        end
        calib.M = cv.initCameraMatrix2D(objectPoints, imagePoints, ...
            opts.imageSize, params{:});
    else
        calib.M = eye(3);
        if opts.flags.FixAspectRatio
            calib.M(1,1) = opts.aspectRatio;
        end
    end
    if opts.flags.TiltedModel
        calib.D = zeros(1,14);
    elseif opts.flags.ThinPrismModel
        calib.D = zeros(1,12);
    elseif opts.flags.RationalModel
        calib.D = zeros(1,8);
    else
        calib.D = zeros(1,5);
    end
    params = st2kv(opts.flags);
    params = [params, 'CameraMatrix',calib.M, 'DistCoeffs',calib.D, ...
        'UseIntrinsicGuess',opts.flags.UseIntrinsicGuess];

    % calibration: find intrinsic and extrinsic camera parameters
    if false
        % we will later manually compute reprojection errors
        [calib.M, calib.D, calib.rms, calib.R, calib.T] = cv.calibrateCamera(...
            objectPoints, imagePoints, opts.imageSize, params{:});
        % placeholder for standard deviations of estimates
        calib.sdInt = nan(1, 18);
        calib.sdExt = nan(1, 6*numel(calib.R));
    else
        % returns reprojection errors (same as computeReprojectionErrors)
        [calib.M, calib.D, calib.rms, calib.R, calib.T, ...
            calib.sdInt, calib.sdExt, calib.rmsPerView] = cv.calibrateCamera(...
            objectPoints, imagePoints, opts.imageSize, params{:});
    end
    ok = all(isfinite([calib.M(:); calib.D(:)]));
end

function saveCameraParams(filename, calib, opts, writeExtrinsics, imagePoints)
    if nargin < 4, writeExtrinsics = false; end

    fs = struct();
    fs.calibration_time = datestr(now());
    if writeExtrinsics
        fs.nframes = int32(numel(calib.R));
    end
    fs.image_width = int32(opts.imageSize(1));
    fs.image_height = int32(opts.imageSize(2));
    fs.board_width = int32(opts.boardSize(1));
    fs.board_height = int32(opts.boardSize(2));
    fs.square_size = opts.squareSize;
    if opts.flags.FixAspectRatio
        fs.aspectRatio = opts.aspectRatio;
    end
    fs.flags = opts.flags;
    fs.camera_matrix = calib.M;
    fs.distortion_coefficients = calib.D;
    if writeExtrinsics
        % set of 6-tuples (rotation vector + translation vector) for each view
        RT = cellfun(@(r,t) [r(:); t(:)]', calib.R, calib.T, ...
            'UniformOutput',false);
        RT = cat(1, RT{:});
        fs.extrinsic_parameters = RT;
    end
    if nargin > 4
        fs.image_points = imagePoints;
    end
    cv.FileStorage(filename, fs);
end

function kv = st2kv(st)
    % convert struct to cell-array of key/value params
    k = fieldnames(st);
    v = struct2cell(st);
    kv = [k(:) v(:)]';
    kv = kv(:)';
end

function displayErrorEstimates(calib)
    D = calib.D;
    if numel(D) < 14, D(14) = 0; end
    sdInt = calib.sdInt;
    if numel(sdInt) < 18, sdInt(18) = NaN; end
    sdExt = reshape(calib.sdExt, 3, 2, []);  % 1/2/3, R/T, N

    fmt = ' %9.4f +/- %-9.4f ';
    fprintf('\n');
    fprintf('\t\t\tStandard Errors of Estimated Camera Parameters\n');
    fprintf('\t\t\t----------------------------------------------\n');
    fprintf('\n');
    fprintf('Intrinsics\n');
    fprintf('----------\n');
    fprintf('Focal length (pixels):    [');
    fprintf(fmt, calib.M(1,1), sdInt(1), calib.M(2,2), sdInt(2));
    fprintf(']\n');
    fprintf('Principal Point (pixels): [');
    fprintf(fmt, calib.M(1,3), sdInt(3), calib.M(2,3), sdInt(4));
    fprintf(']\n');
    fprintf('Radial distortion:        [');
    fprintf(fmt, D(1), sdInt(5), D(2), sdInt(6), D(5), sdInt(9));
    fprintf(']\n');
    fprintf('Tangential distortion:    [');
    fprintf(fmt, D(3), sdInt(7), D(4), sdInt(8));
    fprintf(']\n');
    fprintf('Rational distortion:      [');
    fprintf(fmt, D(6), sdInt(10), D(7), sdInt(11), D(8), sdInt(12));
    fprintf(']\n');
    fprintf('Thin Prism distortion:    [');
    fprintf(fmt, D(9), sdInt(13), D(10), sdInt(14), D(11), sdInt(15), ...
        D(12), sdInt(16));
    fprintf(']\n');
    fprintf('Tilt distortion:          [');
    fprintf(fmt, D(13), sdInt(17), D(14), sdInt(18));
    fprintf(']\n');
    fprintf('\n');
    fprintf('Extrinsics\n');
    fprintf('----------\n');
    fprintf('Rotation vectors:\n');
    for i=1:numel(calib.R)
        fprintf('\t[');
        fprintf(fmt, calib.R{i}(1), sdExt(1,1,i), ...
            calib.R{i}(2), sdExt(2,1,i), calib.R{i}(3), sdExt(3,1,i));
        fprintf(']\n');
    end
    fprintf('Translation vectors (world units):\n');
    for i=1:numel(calib.T)
        fprintf('\t[');
        fprintf(fmt, calib.T{i}(1), sdExt(1,2,i), ...
            calib.T{i}(2), sdExt(2,2,i), calib.T{i}(3), sdExt(3,2,i));
        fprintf(']\n');
    end
end

function [rmseAvg, rmsePerView, err] = computeReprojectionErrors(objectPoints, imagePoints, calib)
    % 3D points projection using camera calibration params
    N = numel(objectPoints);
    imagePoints2 = cell(N,1);
    for i=1:N
        imagePoints2{i} = cv.projectPoints(objectPoints{i}, ...
            calib.R{i}, calib.T{i}, calib.M, 'DistCoeffs',calib.D);
    end

    % compute difference (reprojection errors)
    err = cellfun(@minus, imagePoints, imagePoints2, 'UniformOutput',false);

    % total RMSE from all points, and RMSE per view
    % (same as calib.rms and calib.rmsPerView computed by calibrateCamera)
    if true
        fcnRMSE = @(e) sqrt(mean(sum(e.^2, 2)));
        rmseAvg = fcnRMSE(cat(1, err{:}));
        rmsePerView = cellfun(fcnRMSE, err);
    else
        e = cellfun(@(e) norm(e(:)), err).^2;
        n = cellfun(@(e) size(e,1), err);
        rmseAvg = sqrt(sum(e) / sum(n));
        rmsePerView = sqrt(e ./ n);
    end
end

function [fcn, roi] = buildUndistortFunction(calib, opts)
    % when the scaling parameter Alpha=0, it returns undistorted image
    % with minimum unwanted pixels. So it may even remove some pixels at
    % image corners.
    % When Alpha=1, all pixels are retained with some extra black images.
    % It also returns an image ROI which can be used to crop the result.
    [newM, roi] = cv.getOptimalNewCameraMatrix(calib.M, calib.D, ...
        opts.imageSize, 'Alpha',1);
    if true
        [map1, map2] = cv.initUndistortRectifyMap(calib.M, calib.D, ...
            opts.imageSize, 'NewCameraMatrix',newM);
        fcn = @(img) cv.remap(img, map1, map2, 'Interpolation','Linear');
    elseif true
        fcn = @(img) cv.undistort(img, calib.M, calib.D, 'NewCameraMatrix',newM);
    else
        fcn = @(img) cv.undistort(img, calib.M, calib.D, 'NewCameraMatrix',calib.M);
        roi = [0 0 opts.imageSize];
    end
end

function visualizeReprojErrors(totalAvgErr, perViewErrors, reprojErrs)
    N = numel(reprojErrs);

    % visualize reprojection errors
    re = cat(2, reprojErrs{:});
    plot(re(:,1:2:end), re(:,2:2:end), '+')
    legend(num2str((1:N)', 'image %d')), grid on
    xlabel('X'), ylabel('Y')
    title(sprintf('Reprojection Error (in pixel), RMSE = %f', totalAvgErr))

    % visualize RMSE
    figure, bar(1:N, perViewErrors)
    hLin = line(xlim(), [1 1]*totalAvgErr, 'LineStyle','--', 'Color','r');
    legend(hLin, 'Overall Mean error')
    xlabel('Images'), ylabel('Mean Error (in pixels)')
    title('Mean Reprojection Error per Image')
end

function visualizeExtrinsics(calib, opts)
    N = numel(calib.R);
    clr = lines(N);
    w = (opts.boardSize(1) - 1) * opts.squareSize;
    h = (opts.boardSize(2) - 1) * opts.squareSize;
    s = max(w,h);  % scale in terms of width/height

    % board corner points (in model coordinate system, i.e objectPoints)
    XYZ = [0 0 0; w 0 0; w h 0; 0 h 0; 0 0 0]';

    % axis vector points at origin of world coordinates (camera frame)
    ax = [0 0 0; 1 0 0; 0 0 0; 0 1 0; 0 0 0; 0 0 1]' * (0.6*s);

    % plot axis vectors at the origin
    plot3(ax(1,:), ax(2,:), ax(3,:), 'k', 'LineWidth',2)
    hold on
    text(0.8*s, 0, 0, 'X_c')
    text(0, 0.8*s, 0, 'Y_c')
    text(0, 0, 0.8*s, 'Z_c')
    % for each board
    for i=1:N
        % transformation from model coordinates to real world coordinates
        R = cv.Rodrigues(calib.R{i});
        T = calib.T{i};
        xyz = bsxfun(@plus, R * XYZ, T);
        % plot board and label it
        patch(xyz(1,:), xyz(2,:), xyz(3,:), clr(i,:), 'LineWidth',1, ...
            'FaceColor',clr(i,:), 'EdgeColor',clr(i,:), 'FaceAlpha',0.2);
        text(T(1), T(2), T(3), num2str(i), 'FontSize',12, 'Color',clr(i,:));
    end
    hold off, axis equal, grid on, box on
    title('Extrinsic Parameters Visualization')
    xlabel('X'), ylabel('Y'), zlabel('Z')  % world units (mm)
    if ~mexopencv.isOctave()
        cameratoolbar
        cameratoolbar('SetCoordSys','y')
    else
        %HACK: CAM* functions not implemented in Octave
        rotate3d on
    end
end

function visualizeDistortion(calib, opts)
    % cameraMatrix = [fx 0 cx; 0 fy cy; 0 0 1]
    %
    % * focal lengths   : fx, fy
    % * aspect ratio    : a = fy/fx
    % * principal point : cx, cy
    %
    M = calib.M;

    % distCoeffs = [k1,k2,p1,p2,k3,k4,k5,k6,s1,s2,s3,s4,taux,tauy]
    %
    % * radial distortion     : k1, k2, k3
    % * tangential distortion : p1, p2
    % * rational distortion   : k4, k5, k6
    % * thin prism distortion : s1, s2, s3, s4
    % * tilted distortion     : taux, tauy (ignored here)
    %
    D = calib.D;
    if numel(D) < 14, D(14) = 0; end

    % https://docs.opencv.org/3.2.0/d9/d0c/group__calib3d.html#details
    nstep = 20;
    [u,v] = meshgrid(linspace(0,opts.imageSize(1)-1,nstep), ...
        linspace(0,opts.imageSize(2)-1,nstep));
    xyz = M \ [u(:) v(:) ones(numel(u),1)].';
    xp = xyz(1,:) ./ xyz(3,:);
    yp = xyz(2,:) ./ xyz(3,:);
    r2 = xp.^2 + yp.^2;
    r4 = r2.^2;
    r6 = r2.^3;
    coef = (1 + D(1)*r2 + D(2)*r4 + D(5)*r6) ./ (1 + D(6)*r2 + D(7)*r4 + D(8)*r6);
    xpp = xp.*coef + 2*D(3)*(xp.*yp) + D(4)*(r2 + 2*xp.^2) + D(9)*r2 + D(10)*r4;
    ypp = yp.*coef + D(3)*(r2 + 2*yp.^2) + 2*D(4)*(xp.*yp) + D(11)*r2 + D(12)*r4;
    u2 = M(1,1)*xpp + M(1,3);
    v2 = M(2,2)*ypp + M(2,3);
    du = u2(:) - u(:);
    dv = v2(:) - v(:);
    dr = reshape(hypot(du,dv), size(u));

    % plot
    quiver(u(:)+1, v(:)+1, du, dv)
    hold on
    plot(opts.imageSize(1)/2, opts.imageSize(2)/2, 'x', M(1,3), M(2,3), 'o')
    [C, hC] = contour(u(1,:)+1, v(:,1)+1, dr, 'k');
    clabel(C, hC)
    hold off, axis ij equal tight
    title('Distortion Model'), xlabel('u'), ylabel('v')
end

Camera Calibration

Contents

Theory

Code