Histogram Comparison

In this demo, we show how to:

Sources:

Contents

Theory

To compare two histograms ( and ), first we have to choose a metric () to express how well both histograms match.

OpenCV implements the function cv.compareHist to perform a comparison. It also offers 4 different metrics to compute the matching:

where

and is the total number of histogram bins.

Code

This program:

Load source images (base image and the two other images to compare)

im = {
    'https://docs.opencv.org/3.3.1/Histogram_Comparison_Source_0.jpg'
    'https://docs.opencv.org/3.3.1/Histogram_Comparison_Source_1.jpg'
    'https://docs.opencv.org/3.3.1/Histogram_Comparison_Source_2.jpg'
};
src = cell(3,1);
for i=1:3
    [~,name,ext] = fileparts(im{i});
    fname = fullfile(mexopencv.root(), 'test', [name ext]);
    if exist(fname, 'file') ~= 2
        disp('Downloading image...')
        urlwrite(im{i}, fname);
    end
    src{i} = cv.imread(fname, 'Color',true);
end

also create an image of half the base image

src{4} = src{1}(end/2:end,:,:);
src = src([1 4 2 3]);

show images

names = {'Base', 'Half', 'Test1', 'Test2'};
for i=1:numel(src)
    subplot(2,2,i), imshow(src{i}), title(names{i})
end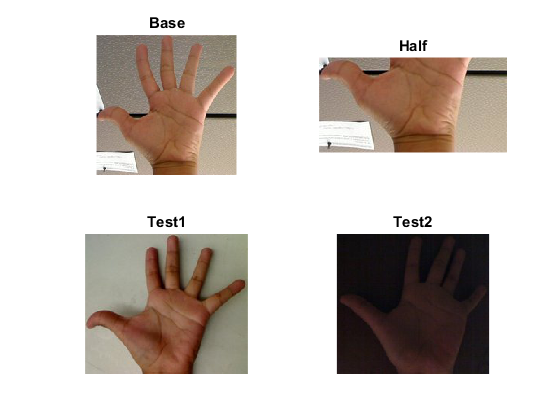

convert images to HSV color space

hsv = cell(size(src));
for i=1:numel(src)
    hsv{i} = cv.cvtColor(src{i}, 'RGB2HSV');
end

calculate H-S 2D histograms

%ranges = {linspace(0,180,50+1), linspace(0,256,60+1)};
ranges = {[0 180], [0 256]};
hsizes = [50, 60];
histo = cell(size(hsv));
for i=1:numel(hsv)
    histo{i} = cv.calcHist(hsv{i}(:,:,1:2), ranges, 'HistSize',hsizes, 'Uniform',true);
    histo{i} = cv.normalize(histo{i}, 'NormType','MinMax', 'Alpha',0, 'Beta',1);
end

compare histogram of the base image against the other histograms using four different metrics

algs = {'Correlation', 'ChiSquare', 'Intersection', 'Bhattacharyya'};
D = zeros(numel(algs),numel(histo));
for j=1:numel(histo)
    for i=1:numel(algs)
        D(i,j) = cv.compareHist(histo{1}, histo{j}, 'Method',algs{i});
    end
end

The first image is the base (to be compared to the others), the other 2 are the test images. We also compare the first image with respect to itself and with respect of half the base image.

We should expect a perfect match when we compare the base image histogram with itself. Also, compared with the histogram of half the base image, it should present a high match since both are from the same source. For the other two test images, we can observe that they have very different lighting conditions, so the matching should not be very good.

Here are the numeric results

if ~mexopencv.isOctave()
    t = array2table(D, 'VariableNames',names, 'RowNames',algs);
    disp(t);
else
    %HACK: use cell array instead of table
    t = [{''}, names; algs(:), arrayfun(@num2str,D,'Uniform',false)];
    t = t';
    fprintf('%13s %9s %9s %9s %9s\n',t{:});
end

                      Base      Half       Test1      Test2  
                     ______    _______    _______    ________
    Correlation           1    0.88752      0.211    0.075794
    ChiSquare             0     4.5964     1360.7      4684.5
    Intersection     18.692     13.001      5.682      2.7757
    Bhattacharyya         0    0.24179    0.66792     0.86341

For the Correlation and Intersection methods, the higher the metric, the more accurate the match. As we can see, the match base-base is the highest of all as expected. Also we can observe that the match base-half is the second best match (as we predicted). For the other two metrics, the less the result, the better the match. We can observe that the matches between the test 1 and test 2 with respect to the base are worse, which again, was expected.