Non-Local Means Image Denoising

In this demo, we will learn:

Sources:

Contents

Theory

We have previously seen many image smoothing techniques like Gaussian Blurring, Median Blurring, etc. and they were good to some extent in removing small quantities of noise. In those techniques, we took a small neighbourhood around a pixel and did some operations like Gaussian weighted average, median of the values, etc. to replace the central element. In short, noise removal at a pixel was local to its neighbourhood.

There is a property of noise. Noise is generally considered to be a random variable with zero mean. Consider a noisy pixel, where is the true value of pixel and is the noise in that pixel. You can take large number of same pixels (say ) from different images and computes their average. Ideally, you should get since mean of noise is zero.

You can verify it yourself by a simple setup. Hold a static camera to a certain location for a couple of seconds. This will give you plenty of frames, or a lot of images of the same scene. Then write a piece of code to find the average of all the frames in the video. Compare the final result and first frame. You can see reduction in noise. Unfortunately this simple method is not robust to camera and scene motions. Also often there is only one noisy image available.

So idea is simple, we need a set of similar images to average out the noise. Consider a small window (say 5x5 window) in the image. Chance is large that the same patch may be somewhere else in the image. Sometimes in a small neigbourhood around it. What about using these similar patches together and find their average? For that particular window, that is fine. See an example image below:

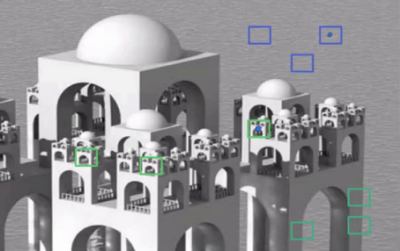
The blue patches in the image looks the similar. Green patches looks similar. So we take a pixel, take small window around it, search for similar windows in the image, average all the windows and replace the pixel with the result we got. This method is Non-Local Means Denoising. It takes more time compared to blurring techniques we saw earlier, but its result is very good. More details and online demo can be found in the following resources:

For color images, image is converted to CIELAB colorspace and then it separately denoise L and AB components.

OpenCV provides four variations of this technique:

Common arguments are:

1) cv.fastNlMeansDenoising, cv.fastNlMeansDenoisingColored

First we show how to remove noise from color/grayscale images. (Noise is expected to be gaussian).

Options

do_color = true;
do_noise_gauss = true;
do_noise_saltnpepper = false;

Image

Load image (either grayscale or color)

src = cv.imread(fullfile(mexopencv.root(),'test','lena.jpg'), 'Color',do_color);
dst = src;

Noise

Add Gaussian noise

if do_noise_gauss
    m = 0;                                  % noise mean
    sd = 0.4 * std(double(dst(:)) / 255);   % noise standard deviation
    if mexopencv.require('images')
        dst = imnoise(dst, 'gaussian', m, sd^2);
    else
        noise = randn(size(dst)) * sd + m;
        dst = double(dst)/255 + noise;
        dst = min(max(dst, 0), 1);
        dst = uint8(dst * 255);
    end
end

Add Salt & Pepper noise

if do_noise_saltnpepper
    prcnt = 0.01;  % noise density
    if mexopencv.require('images')
        dst = imnoise(dst, 'salt & pepper', prcnt);
    else
        mask = rand(size(dst));
        dst(mask < prcnt/2) = 0;
        dst(mask > 1 - prcnt/2) = 255;
    end
end

Show noisy image

subplot(121), imshow(src), title('original')
subplot(122), imshow(dst), title('noisy')
fprintf('PSNR = %.6f\n', cv.PSNR(src, dst));

PSNR = 20.896842

Denoise

Compare various image denoise techniques

imgs = cell(5,1);
names = cell(size(imgs));
for i=1:numel(imgs)
    tic
    switch i
        case 1
            str = 'Box Filter';
            out = cv.boxFilter(dst, 'KSize',[7 7]);
        case 2
            str = 'Gaussian Filter';
            out = cv.GaussianBlur(dst, 'KSize',[7 7], 'SigmaX',5, 'SigmaY',5);
        case 3
            str = 'Median Filter';
            out = cv.medianBlur(dst, 'KSize',3);
        case 4
            str = 'Bilateral Filter';
            out = cv.bilateralFilter(dst, 'Diameter',7, 'SigmaColor',35, 'SigmaSpace',5);
        case 5
            str = 'Non-Local Means Filter';
            if size(dst,3) == 1
                out = cv.fastNlMeansDenoising(dst, 'H',9);
            else
                out = cv.fastNlMeansDenoisingColored(dst, 'H',9, 'HColor',9);
            end
    end
    t = toc;
    imgs{i} = out;
    names{i} = str;
    fprintf('%-23s : [PSNR = %.6f] Elapsed time is %f seconds.\n', ...
        str, cv.PSNR(src, out), t);
end

Box Filter              : [PSNR = 27.064057] Elapsed time is 0.032708 seconds.
Gaussian Filter         : [PSNR = 27.272195] Elapsed time is 0.020858 seconds.
Median Filter           : [PSNR = 27.257955] Elapsed time is 0.053008 seconds.
Bilateral Filter        : [PSNR = 24.196976] Elapsed time is 0.044703 seconds.
Non-Local Means Filter  : [PSNR = 25.448762] Elapsed time is 1.178667 seconds.

Show results

for i=1:numel(imgs)
    figure, imshow(imgs{i}), title(names{i})
end

Show as movie for easy comparison

if ~mexopencv.isOctave() && mexopencv.require('images')
    %HACK: IMPLAY not implemented in Octave
    for i=1:numel(imgs)
        imgs{i} = cv.putText(imgs{i}, names{i}, [10 20], ...
            'Color',[255 255 0], 'LineType','AA', ...
            'FontFace','HersheyPlain', 'FontScale',1.2);
    end
    implay(cat(4, imgs{:}), 1)
end

2) cv.fastNlMeansDenoisingMulti

Now we will apply the same method to a video.

In that case, a total of temporalWindowSize frames are used where central frame is the frame to be denoised. For example, you passed a list of 5 frames as input. Let imgToDenoiseIndex = 2 and temporalWindowSize = 3. Then frame-1, frame-2 and frame-3 are used to denoise frame-2.

Video

Open input video

if ~mexopencv.isOctave() && mexopencv.require('images')
    fname = fullfile(toolboxdir('images'), 'imdata', 'AT3_1m4_%02d.tif');
else
    fname = fullfile(mexopencv.root(), 'test', '768x576.avi');
end
cap = cv.VideoCapture(fname);
assert(cap.isOpened());

Noise

Read first 10 frames, and create noisy frames

len = 10;
srcs = cell(len,1);
dsts = cell(len,1);
for i=1:len
    % get frame and convert to grayscale
    src = cap.read();
    assert(~isempty(src));
    src = cv.cvtColor(src, 'RGB2GRAY');
    srcs{i} = src;

    % add Gaussian noise
    noise = randn(size(src)) * 10;
    dst = double(src) + noise;
    dst = min(max(dst, 0), 255);
    dst = uint8(dst);
    dsts{i} = dst;
end

cap.release();

Denoise

Denoise each frame considering 5 nearby frames

out = cell(len,1);
for i=1:len
    tic
    if i > 2 && i < len-1
        out{i} = cv.fastNlMeansDenoisingMulti(dsts, i-1, 5, 'H',6, ...
            'TemplateWindowSize',7, 'SearchWindowSize',35);
    else
        % skip images on the timeline border with insufficient neighbors
        out{i} = dsts{i};
    end
    toc
end

Elapsed time is 0.001082 seconds.
Elapsed time is 0.000352 seconds.
Elapsed time is 2.658743 seconds.
Elapsed time is 2.733849 seconds.
Elapsed time is 2.602693 seconds.
Elapsed time is 2.631372 seconds.
Elapsed time is 2.557090 seconds.
Elapsed time is 2.659948 seconds.
Elapsed time is 0.001488 seconds.
Elapsed time is 0.000062 seconds.

Show results for the 3rd frame

figure
subplot(221), imshow(srcs{3}), title('original')
subplot(222), imshow(dsts{3}), title('noisy')
subplot(223), imshow(out{3}), title('denoised')

Show as movie

if ~mexopencv.isOctave() && mexopencv.require('images')
    implay(cat(4, out{:}), 1)
end