PCA for dimensionality reduction

An example using PCA for dimensionality reduction while maintaining an amount of variance.

This program demonstrates how to use OpenCV PCA with a specified amount of variance to retain.

The program takes as input a list of images. The author recommends using the first 15 faces of the AT&T face data set: http://www.cl.cam.ac.uk/research/dtg/attarchive/facedatabase.html

Sources:

Contents

Input images

get the list of images

dname = fullfile(mexopencv.root(), 'test', 'att_faces');
if isdir(dname)
    % NOTE: run facerec_demo.m to download dataset
    imgList = arrayfun(@(i) fullfile(['s' int2str(i)], '1.pgm'), 1:15, ...
        'UniformOutput',false);
else
    dname = fullfile(mexopencv.root(), 'test');
    imgList = dir(fullfile(dname, 'left*.jpg'));
    imgList = {imgList.name};
end
imgList = cellfun(@(f) fullfile(dname, f), imgList(:), 'UniformOutput',false);
display(imgList)

imgList =
  15×1 cell array
    'C:\Users\Amro\Desktop\mexopencv\test\att_faces\s1\1.pgm'
    'C:\Users\Amro\Desktop\mexopencv\test\att_faces\s2\1.pgm'
    'C:\Users\Amro\Desktop\mexopencv\test\att_faces\s3\1.pgm'
    'C:\Users\Amro\Desktop\mexopencv\test\att_faces\s4\1.pgm'
    'C:\Users\Amro\Desktop\mexopencv\test\att_faces\s5\1.pgm'
    'C:\Users\Amro\Desktop\mexopencv\test\att_faces\s6\1.pgm'
    'C:\Users\Amro\Desktop\mexopencv\test\att_faces\s7\1.pgm'
    'C:\Users\Amro\Desktop\mexopencv\test\att_faces\s8\1.pgm'
    'C:\Users\Amro\Desktop\mexopencv\test\att_faces\s9\1.pgm'
    'C:\Users\Amro\Desktop\mexopencv\test\att_faces\s10\1.pgm'
    'C:\Users\Amro\Desktop\mexopencv\test\att_faces\s11\1.pgm'
    'C:\Users\Amro\Desktop\mexopencv\test\att_faces\s12\1.pgm'
    'C:\Users\Amro\Desktop\mexopencv\test\att_faces\s13\1.pgm'
    'C:\Users\Amro\Desktop\mexopencv\test\att_faces\s14\1.pgm'
    'C:\Users\Amro\Desktop\mexopencv\test\att_faces\s15\1.pgm'

read in the data

images = cellfun(@imread, imgList, 'UniformOutput',false);
sz = size(images{1});
assert(numel(images) >= 2, ...
    ['This demo needs at least 2 images to work. ' ...
    'Please add more images to your data set!']);
assert(ndims(sz) == 2, 'Expects grayscale images');

preview images

if mexopencv.require('images')
    montage(cat(4, images{:}));
end

PCA

Reshape and stack images into a row Matrix

data = zeros(numel(images), prod(sz));
for i=1:numel(images)
    data(i,:) = double(images{i}(:)) / 255;
end
whos data

  Name       Size                 Bytes  Class     Attributes

  data      15x10304            1236480  double              

perform PCA

RET_VAR = 95;
pca = cv.PCA(data, 'DataAs','Row', 'RetainedVariance',RET_VAR/100);
display(pca)

pca = 
  PCA with properties:

              id: 7
    eigenvectors: [11×10304 double]
     eigenvalues: [11×1 double]
            mean: [1×10304 double]

display the "average image"

figure, imshow(reshape(pca.mean, sz), []), title('mean')

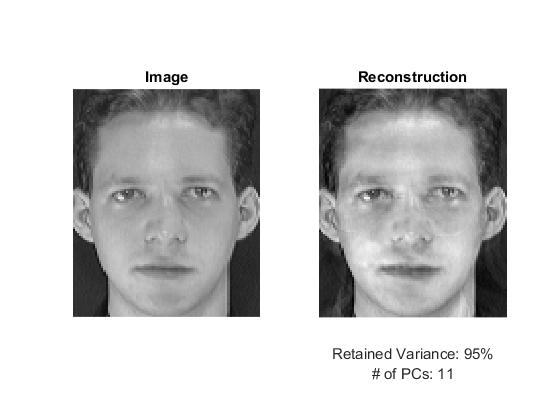
Demonstration of the effect of retainedVariance on the first image

% project into the eigenspace, thus the image becomes a "point"
img1 = data(1,:);
point = pca.project(img1);

% re-create the image from the "point"
img1R = pca.backProject(point);

% reshape from a row vector into image shape
img1R = reshape(img1R, sz);

% re-scale for displaying purposes
if true
    img1R = cv.normalize(img1R, ...
        'NormType','MinMax', 'Alpha',0, 'Beta',255, 'DType','uint8');
else
    img1R = (img1R - min(img1R(:))) ./ (max(img1R(:)) - min(img1R(:)));
    img1R = uint8(img1R * 255);
end

% display result
figure
subplot(121), imshow(reshape(img1,sz)), title('Image')
subplot(122), imshow(img1R), title('Reconstruction')
xlabel({sprintf('Retained Variance: %d%%',RET_VAR);
    sprintf('# of PCs: %d', size(pca.eigenvectors,1))})