Principal Component Analysis (PCA)
In this demo, you will learn how to use the OpenCV class cv.PCA to calculate the orientation of an object.
Sources:
Contents
Theory
Principal Component Analysis (PCA) is a statistical procedure that extracts the most important features of a dataset.

Consider that you have a set of 2D points as it is shown in the figure above. Each dimension corresponds to a feature you are interested in. Here some could argue that the points are set in a random order. However, if you have a better look you will see that there is a linear pattern (indicated by the blue line) which is hard to dismiss. A key point of PCA is the Dimensionality Reduction. Dimensionality Reduction is the process of reducing the number of the dimensions of the given dataset. For example, in the above case it is possible to approximate the set of points to a single line and therefore, reduce the dimensionality of the given points from 2D to 1D.
Moreover, you could also see that the points vary the most along the blue line, more than they vary along the Feature 1 or Feature 2 axes. This means that if you know the position of a point along the blue line you have more information about the point than if you only knew where it was on Feature 1 axis or Feature 2 axis.
Hence, PCA allows us to find the direction along which our data varies the most. In fact, the result of running PCA on the set of points in the diagram consist of 2 vectors called eigenvectors which are the principal components of the data set.

The size of each eigenvector is encoded in the corresponding eigenvalue and indicates how much the data vary along the principal component. The beginning of the eigenvectors is the center of all points in the data set. Applying PCA to N-dimensional data set yields N N-dimensional eigenvectors, N eigenvalues and 1 N-dimensional center point.
Now we will see how the eigenvectors and eigenvalues are computed.
The goal is to transform a given data set ![]() of dimension
of dimension ![]() to an alternative data set
to an alternative data set ![]() of smaller dimension
of smaller dimension ![]() . Equivalently, we are seeking to find the matrix
. Equivalently, we are seeking to find the matrix ![]() , where
, where ![]() is the Karhunen-Loeve transform (KLT) of matrix
is the Karhunen-Loeve transform (KLT) of matrix ![]() :
:
![]()
1) Organize the data set
Suppose you have data comprising a set of observations of ![]() variables, and you want to reduce the data so that each observation can be described with only
variables, and you want to reduce the data so that each observation can be described with only ![]() variables,
variables, ![]() . Suppose further, that the data are arranged as a set of
. Suppose further, that the data are arranged as a set of ![]() data vectors
data vectors ![]() with each
with each ![]() representing a single grouped observation of the
representing a single grouped observation of the ![]() variables.
variables.
- Write
 as row vectors, each of which has
as row vectors, each of which has 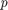 columns.
columns.
- Place the row vectors into a single matrix
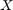 of dimensions
of dimensions 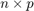 .
.
2) Calculate the empirical mean
- Find the empirical mean along each dimension
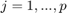 .
.
- Place the calculated mean values into an empirical mean vector
 of dimensions
of dimensions 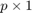 .
.
![]()
3) Calculate the deviations from the mean
Mean subtraction is an integral part of the solution towards finding a principal component basis that minimizes the mean square error of approximating the data. Hence, we proceed by centering the data as follows:
- Subtract the empirical mean vector
 from each row of the data matrix
from each row of the data matrix 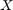 .
.
- Store mean-subtracted data in the
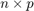 matrix
matrix 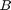 .
.
![]()
where ![]() is an
is an ![]() column vector of all 1s:
column vector of all 1s:
![]()
4) Find the covariance matrix
- Find the
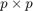 empirical covariance matrix
empirical covariance matrix 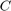 from the outer product of matrix
from the outer product of matrix 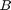 with itself:
with itself:
![]()
where ![]() is the conjugate transpose operator. Note that if
is the conjugate transpose operator. Note that if ![]() consists entirely of real numbers, which is the case in many applications, the "conjugate transpose" is the same as the regular
transpose.
consists entirely of real numbers, which is the case in many applications, the "conjugate transpose" is the same as the regular
transpose.
5) Find the eigenvectors and eigenvalues of the covariance matrix
- Compute the matrix
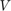 of eigenvectors which diagonalizes the covariance matrix
of eigenvectors which diagonalizes the covariance matrix 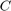 :
:
![]()
where ![]() is the diagonal matrix of eigenvalues of
is the diagonal matrix of eigenvalues of ![]() .
.
- Matrix
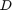 will take the form of an
will take the form of an 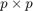 diagonal matrix:
diagonal matrix:
![]()
here, ![]() is the
is the ![]() -th eigenvalue of the covariance matrix
-th eigenvalue of the covariance matrix ![]()
- Matrix
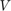 , also of dimension
, also of dimension 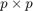 , contains
, contains 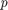 column vectors, each of length
column vectors, each of length 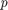 , which represent the
, which represent the 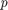 eigenvectors of the covariance matrix
eigenvectors of the covariance matrix 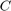 .
.
- The eigenvalues and eigenvectors are ordered and paired. The
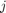 -th eigenvalue corresponds to the
-th eigenvalue corresponds to the 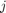 th eigenvector.
th eigenvector.
Code
function pca_intro_demo()Load image
fname = fullfile(mexopencv.root(), 'test', 'pca_test1.jpg'); if exist(fname, 'file') ~= 2 disp('Downloading image...') url = 'https://cdn.rawgit.com/opencv/opencv/3.2.0/samples/data/pca_test1.jpg'; urlwrite(url, fname); end src = cv.imread(fname, 'Color',true);
Convert image to binary
bw = cv.threshold(cv.cvtColor(src,'RGB2GRAY'), 'Otsu');
Find all the contours in the thresholded image
[contours, hierarchy] = cv.findContours(bw, 'Mode','List', 'Method','None'); for i=1:numel(contours) % Calculate the area of each contour a = cv.contourArea(contours{i}); if a < 1e2 || a > 1e5 % Ignore contours that are too small or too large continue; end % Draw each contour only for visualisation purposes src = cv.drawContours(src, contours, 'Hierarchy',hierarchy, ... 'ContourIdx',i-1, 'MaxLevel',0, 'Color',[255 0 0], 'Thickness',2); % Find the orientation of each shape [src, ang] = getOrientation(src, contours{i}); fprintf('Contour #%d orientation = %.1f degrees\n', i, -ang*(180/pi)); end
Show result
imshow(src)

endHelper functions
function [img, angl] = getOrientation(img, pts) %GETORIENTATION Extract object orientation using PCA % Perform PCA analysis data points arranged as Nx2 pts = cat(1, pts{:}); obj = cv.PCA(pts); % Draw the object center of mass img = cv.circle(img, obj.mean, 3, 'Color',[255 0 255], 'Thickness',2); % Draw the principal components (each eigenvector is multiplied by its % eigenvalue and translated to the mean position) s = 0.02 * bsxfun(@times, obj.eigenvectors, obj.eigenvalues); img = drawAxisArrow(img, obj.mean, obj.mean + s(1,:), 1, ... 'Color',[0 255 0], 'LineType','AA'); img = drawAxisArrow(img, obj.mean, obj.mean - s(2,:), 5, ... 'Color',[0 255 255], 'LineType','AA'); % Orientation in radians [-pi,pi] angl = atan2(obj.eigenvectors(1,2), obj.eigenvectors(1,1)); end function img = drawAxisArrow(img, p, q, sc, varargin) %DRAWAXISARROW Draw principal component axis line if nargin < 4, sc = 0.2; end % Compute angle (in radians) and hypotenuse v = p - q; ang = atan2(v(2), v(1)); mag = hypot(v(2), v(1)); % Here we lengthen the arrow by a factor of scale, % and draw the main line of the arrow q = p - sc * mag * [cos(ang), sin(ang)]; img = cv.line(img, p, q, varargin{:}); % Now we draw the tips of the arrow. We do some scaling so that the % tips look proportional to the main line of the arrow p = q + 9 * [cos(ang + pi/4), sin(ang + pi/4)]; img = cv.line(img, p, q, varargin{:}); p = q + 9 * [cos(ang - pi/4), sin(ang - pi/4)]; img = cv.line(img, p, q, varargin{:}); end
Contour #1 orientation = 14.9 degrees Contour #2 orientation = 13.5 degrees Contour #3 orientation = 12.7 degrees Contour #4 orientation = 9.7 degrees Contour #5 orientation = -86.5 degrees Contour #6 orientation = 9.8 degrees
References
And special thanks to Svetlin Penkov for the original tutorial.