Contents

Squares Detector

It loads several images sequentially and tries to find squares in each image.

A program using pyramid scaling, Canny, contours, and contour simpification (it's got it all folks) to find squares in a list of images pic*.png. Returns sequence of squares detected on the image.

Sources:

function squares_detector_demo()

loop over sequence of images

    names = cv.glob(fullfile(mexopencv.root(), 'test', 'pic*.png'));
    for i=1:numel(names)

load image

        img = cv.imread(names{i}, 'Color',true);

find and draw squares (TODO: apply something like groupRectangles)

        squares = findSquares(img);
        if true
            img = cv.polylines(img, squares, 'Closed',true, ...
                'Color',[255 0 255], 'Thickness',2, 'LineType','AA');
        else
            img = cv.drawContours(img, squares, ...
                'Color',[255 0 255], 'Thickness',2, 'LineType','AA');
        end

show result

        [~,fname,ext] = fileparts(names{i});
        figure, imshow(img), title([fname ext])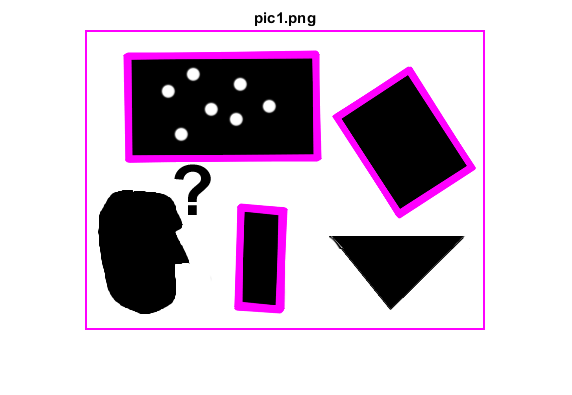

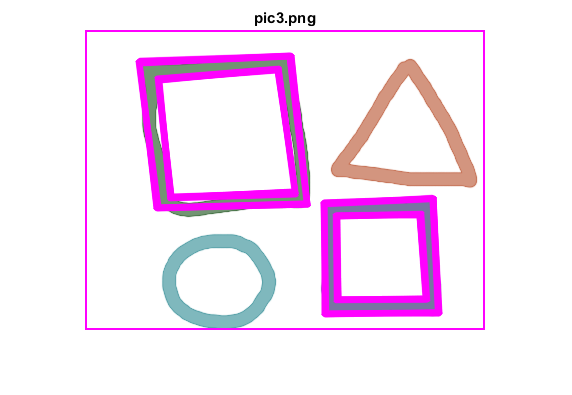
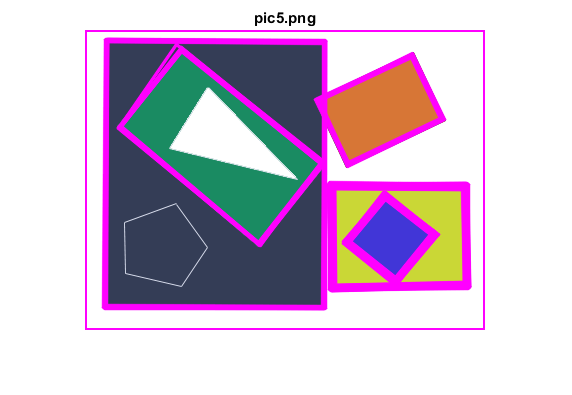
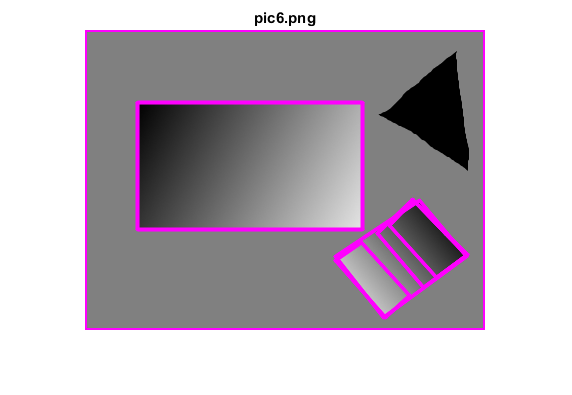
    end

end

Helper functions

function squares = findSquares(img)
    if true
        % down-scale and upscale the image to filter out the noise
        sz = size(img);
        img = cv.pyrDown(img, 'DstSize',fix(sz([2 1])/2));
        img = cv.pyrUp(img, 'DstSize',sz([2 1]));
    else
        img = cv.GaussianBlur(img, 'KSize',[5 5]);
    end

    % find squares in every color plane of the image
    squares = {};
    for ch=1:size(img,3)
        % try several threshold levels
        N = 11;
        thresh = 50;
        for t=1:N
            if t == 1
                % apply Canny (helps to catch squares with gradient shading).
                % Take the upper threshold from slider and set the lower to 0
                % (which forces edges merging)
                gray = cv.Canny(img(:,:,ch), [0 thresh], 'ApertureSize',5);
                % dilate to remove potential holes between edge segments
                gray = cv.dilate(gray);
            else
                % apply threshold if not first threshold level
                gray = cv.threshold(img(:,:,ch), t*255/N, 'Type','Binary');
            end

            % find and test each contour
            contours = cv.findContours(gray, 'Mode','List', 'Method','Simple');
            for i=1:numel(contours)
                % approximate contour with accuracy proportional to its perimeter
                alen = cv.arcLength(contours{i}, 'Closed',true);
                approx = cv.approxPolyDP(contours{i}, ...
                    'Epsilon',alen*0.02, 'Closed',true);

                % to be a square/rectangle, a contour should have:
                %
                % * 4 vertices after approximation,
                % * relatively large area (to filter out noisy contours),
                % * be convex.
                %
                % Note: we take absolute value of area because it can be
                % positive or negative, according to contour orientation
                if numel(approx) == 4 && ...
                    abs(cv.contourArea(approx)) > 1000 && ...
                    cv.isContourConvex(approx)
                    % find the maximum cosine of angles between joint edges
                    idx0 = 2:4;                % current
                    idx1 = modulu4(idx0 + 1);  % next
                    idx2 = modulu4(idx0 - 1);  % previous
                    maxCosine = max(abs(cellfun(@cosineAngle, ...
                        approx(idx0), approx(idx1), approx(idx2))));

                    % if cosines of all angles are small (~90 degree angles),
                    % then write quandrange vertices to resultant sequence
                    if maxCosine < 0.3  % acosd(0.3) ~ 72.5 degrees
                        squares{end+1} = approx;
                    end
                end
            end
        end
    end
end

function cosine = cosineAngle(pt0, pt1, pt2)
    % find cosine of angle between vectors from pt0->pt1 and from pt0->pt2
    % cos(theta) = a.b / ||a|| * ||b||
    vec1 = (pt1 - pt0);
    vec2 = (pt2 - pt0);
    cosine = dot(vec1, vec2) / (norm(vec1) * norm(vec2));
end

function idx = modulu4(idx)
    idx = mod(idx - 1, 4) + 1;
end